Dan Geer at SFI

"Optimality and Fragility on the Internet"

Similar lecture available in video here and print here.

• There are 3 professions that “beat practitioners into a state of humility—farming, weather, cyber security.”
• Cybersecurity—there is a dual use inherent to all internet tools.
• Offensive protection is where expensive innovation is happening today.
• There is an outcome differential between good
• “The most appealing ideas are not important, the most important ideas are not appealing.”
• 10% of all internet traffic is unidentifiable by protocol, and more identification is simply not accurate.
• Between security, convenience and freedom we can choose two, maybe, but not all three.
• Some suggestions to help:
  • 1 Mandatory reporting—CDC has it with regard to disease appearances and they store data with skillful analysis. It would make sense to have mandatory reporting for cybersecurity problems. With real problems, hacks, require them to be reported. With attempted hacks/near misses we can build a reporting system like the FAA has for near misses. Let people report this anonymously and get voluntary entrants into the program. 
  • 2 Network neutrality—is Internet access an information or a communication service? So far we have not named it a communication service, but in reality, which is it? This has consequences for whether there will be common carrier protection or a duty to monitor. Right now, ISPs have it both ways. They should get one or the other, not both.
  • 3 Source code liability—“Security will be exactly as bad as it can be and still function.” There should be software liability regulation. “Intent or willfulness.” Build only liability for intent, not unintentional.
  • 4 Strike back—research the attacker, build cyber smartbombs to learn about them. The issue here is the shared infrastructure.
  • 5 Fall back on resilience. The code base on low-end routers today is 4-5 years old. Many networked components use old technology. Embedded systems should not be immortal.
  • 6 Vulnerability finding has been a good job for 8/9 years. We as a society should buy out (overpay) for finding vulnerabilities. This can expand the talent pool of vulnerability finding. Are “vulns” scarce or dense? “Exploitable areas are scarce enough.”
  • 7 Right to be forgotten. “We are all intelligence agents now…all our digital exhaust is identifiable.” Misrepresentation of identity online is getting harder and harder. The CIA wouldn’t have to fabricate an identity anymore, they can borrow one close to what they need. The new EU rule on this is appropriate, but doesn’t go far enough. “In public” means something very different today, than in the recent past.
  • 8 Internet voting. Most experts think it’s a bad idea.
  • 9 Abandonment. If a company abandons a code base (like Microsoft or Apple pulling support of an old OS), then it should become open source.
  • 10 Convergence. Are the physical and digital one world or 2? They are converging rapidly today. Need to ask “on whose terms will convergence occur?” The cause of risk today is dependence. We will be secure if there can be no unmitigable surprises.
• Security breaches/viruses follow power law distribution. Target and Home Depot both fit on the curve.

Juan Enriquez at SFI

"Are Humans Optimal?"

• Historically on the planet there have been several hominins existing at a time. Right now humans are the only species of hominins.
  • Typically when there is only one species, that is a sign of impending extinction.
• The difference between humans and Neanderthals is less than 0.004% on the genomic level.
  • Differences are in sperm, testes, smell and skin
• There was an experiment in Russia to try and breed domesticated wild foxes. They took only the friendliest foxes and bred them amongst each other. Within a few generations they got tame and were worthy of being pets (more on that here).
• We can now sequence and acquire genetic data 3x quicker than our capacity to store it. We’ve sequenced about 10,000 human genes today. We will start to find more differences soon.
  • One finding is with the ACE gene. No one has climbed Everest without it. 
  • Another is the 577R gene. All male Olympians in power sports have it, others don’t.
• Life is imperfectly transmitted code.
• We can now build just mouth teeth (or human teeth with stem cells from a lost tooth). We can build an ear, a bladder, a trachea.
• Homo evolutis:
  • For better or worse, we’re beginning to control our own evolution
  • This is “unnatural selection or actual intelligent design”
  • We have to live with the consequences, whether they be good or bad.
  • So far, using these technologies we have taken ourselves out of the food chain and doubled lifespans. In this respect, it’s been good for us so far.
• While we conventionally speak about how great the digital revolution has been, the revolution in life sciences is and will be magnitudes greater.
• Co-founded Synthetic Genomics with J. Craig Venter (One of the first to have sequenced the human genome)
  • Synthetic Genomics has developed a cell built that can operate like a computer system. It’s a cell that executes life code.
  • It may be possible to reprogram a species to become another species.
  • It’s like a software that makes its own hardware.
  • Algae is the best scalable production systems for energy development in a constrained world.
• “We are evolving ourselves.” In science, “there are decades when nothing happens and weeks when everything happens.” (a questioner in the audience pointed out this quote comes from Lenin).
• Q: “Do we have secular stagnation?”
  • Enriquez: A resounding no. Today there are people who are smart, creative, with scale and ambition. Lots of great things are happening in the sciences. We are as advanced as ever, and increasingly so. 1 problem is that with technology, our interest in sex different than it used to be, and sex is not keeping the developed world population moving upwards fast enough.

John Doyle at SFI

"Universal Laws and Architectures for Robust Efficiency in Nets, Grids, Bugs, Hearts and Minds"

• By making things more efficient you make things worse
• Architecture flexibility achieves what is possible
• Heroes: Darwin and Touring, dynamics and feedback
• Efficiency and robustness are 2 aspects we want.
  • Sustainable=robust + efficient
• Antifragile=adaptability and evolvability. 
  • Concrete, verifiable, testable.
  • “It’s much easier to bullshit at the macro level than micro.” 
• Robustness, efficient and adaptive. 

• What makes us robust is controlled and acute, what makes us fragile are those same features when they are uncontrolled and chronic.

• Robust efficiency is at the heart of these trade-offs. 
  • On the cell level, we are robust in energy and efficient in energy use.
  • Big fragilities are unintended consequences of mechanisms designed for robustness. 
  • There are tradeoffs between the two. 
  • Fragility is due to the “hijacking” of robustness.
• In the human transition to bipedialism, we became four times more efficient at running distance than chimps, but chimps are faster, better off in the shorter distances.
  • Similarly, if we go on a bike, we are 2x as fast as walking, but more fragile. 
  • Further, we can’t simply “add” a bike to ourselves to gain this speed. 
  • We must add the bike + learn how to ride it.
• There was a visual demonstration, but for the purposes of these notes: imagine there is a wand that can get smaller or larger (or even better, try this with a pen). 
  • You can either hold it in your hand downwards, or balance it on top of your hand upwards (the balancing upwards is nearly impossible with the pen, though that’s part of the point).
  • Down is easy to control, up is hard and destabilizing. 
  • Up and looking away (ie don’t look at your hand, but look elsewhere entirely) is nearly impossible.
  • Gravity is a law. 
    • When we hold the wand downward, gravity is stabilizing. 
    • Stabilizing insofar as it holds it steady and straight. Gravity is destabilizing when holding it up.
  • Down=the easiest, up=harder, up and short want=the hardest (that’s why you can’t balance the pen upwards!).
• We can look at the entropy rate exp(pt).  This explains quantitatively something qualitatively through a law.
• Fragility depends on function (balanced movement in the case of the wand) and specific perturbation. 
• There are hard tradeoffs between optimal lengths, but looking away is simply bad design.
• Without an actuator, variability or extreme variability brings a crash imminently.
• Markets are robust to prices, fragile to all else. 
  • For robustness, we want them to be fast and flexible, but these features cause the fragilities.
  • Much of nature is built on layered architecture between fast “apps” and robust hardware.
  • There are often horizontal transfers from one architecture to another, but only occasional novelty (think about the passing of genes vs the creation of new genes entirely; or similarly the passing of ideas from one discipline to another vs the discovery of novel ideas entirely). This accelerates evolution.
  • Such a system is fragile to exploitation. The more monoculture, the more this is amplified.
  • Our greatest fragility as a society are bad memes. People believe false, dangerous, unhealthy things.
  • These features are shared architectures between genes, bacteria, memes and hardware.
• Hold your hand in front of your face. Move your hand back and forth real fast until the image blurs. Then hold your hand still, and move your head back and forth real fast until your hand blurs. (do this before reading on)
  • Notice that when you turn your head real fast it’s very challenging to get the hand to blur. This is because we have what is called the vestibular ocular reflex.
  • The illusion of speed and flexibility has been tuned to a specific environment. The head is automatically stabilized to see the hand clearly while moving. This is all happening subconsciously in the cerebellum.
• There was another demonstration using colored circles that were adjacent at the midpoint of a screen. The slide was quickly switched and the color lingered for a while in your vision. (I was so intrigued by this, I did some googling afterwards and found the term afterimages. While I could not find the exact demonstration, this one using the American flag is quite cool and gives a sense of the effect covered for the following few lines).Color is the slowest transition. We don’t truly see in color, we simulate it.
  • This is a slow, inflexible, but cheap system (it doesn’t use a lot of resources)
  • It’s tuned to a highly specific environment, so we don’t notice it (it feels totally natural to us)
  • It is fragile to some environments, like the afterimage, but hopefully we don’t encounter that fragility in a context where it can hurt us.
• Learning generally speaking is slow, so we have to evolve reflexes to go fast.

Cris Moore at SFI

Cris Moore

Optimization From Mt. Fuji to the Rockies: How computer scientists and physicists think about optimization, landscapes, phase transitions and fragile models

• We need to make qualitative distinctions between problems
  • There is a Hamiltonian Path Problem—can you visit every node on a graph just once
  • You can do this by a “search tree” until you end up stuck. Go back to the prior node, then begin again. This is called “exhaustive search.
  • ”There is reason to believe that exhaustive search is the only way to solve such a problem
• NP (complete)
  • P: polynomial-can find solutions efficiently
  • NP: we can check a solution efficiently
  • There is a gap between what you can check vs what you can find efficiently. This is the P vs NP problem.
  • Polynomials don’t grow too badly as n grows, but NP complete, if n grows at 2^n then when n=90 it takes longer than the age of the universe to solve.
• When is there a shortcut? 
  • 1: divide and conquer—when there are independent sub-problems. 
  • 2: dynamic programming—sub-problems that are not completely dependent, but become so after we make some choices. (ie there are n nodes to the experiment, but once you take on node the next step becomes independent of the prior choices).
  • 3: When greed is good—minimum spanning tree. Take the shortest edge (ie if you want to build power lines connecting cities, build the shortest connections first until a tree is built).
    • Landscape (imagine a mountain range where your goal is to get to a distant highest peak) a single optimum, that we can find by climbing (no wrong way).
    • Traveling salesman—big shortcuts can lead us down a primrose path. 

•  
  •  
    • There are many local optima where we can get stuck and it’s impossible to figure out the global optimum
• NP completeness=a worst case notion.
  • We assume instances are designed by an adversary to encode hard problems. This is a good assumption in cryptography, but not in most of nature. We must ask: “What kind of adversary are scientists fighting against…Manichean or Augustinian?”
  • The real world has structure. We can start with a “greedy tour” and make modifications until it becomes clear there is nothing more to gain.
• Optimization problems are like exploring high dimensional jewelry (multi-faceted)
  • Simplex—crawls the edges quickly. Takes exponential amounts of time in the worst case, but is efficient in practice.
  • 1: Add noise to the problem and the number of facets goes down
  • 2: “Probably approximately correct”—not looking for the best solution, just a really good one
    • Landscapes are not as dumpy as they could be. Good solutions are close to the optimum, but we might not find THE optimum.  If your data has clusters, any good cluster should be close to the best.
    • There are phase transitions in NP Complete (what are called tipping points)
  • 3: “Sat(isfiability)”—n variables that can be true or false and a formula of constraints with three variables each.  With n variables, 2^n possibilities. We can search, see if it works.  
    • What if constraints are chosen randomly instead of by an adversary? When the density of constraints is too high, we can no longer satisfy them all at once.
• There is a point of transition from unsolvability to solvability
  • The hardest problems to solve are in the transition.  When a problem is no longer solvable, have to search all options to figure that out. 
    • Easy, hard, frozen—the structure gets more fragile the closer you get to the solution.
• Big data and fragile problems:
  • Finding patterns (inference)
  • You actually don’t want the “best” model, as the “best” gives a better fit, but is subject to overfitting and thus does worse with generalizations about the future. 
• Finding communities in networks (social media) is an optimization problem. You can divide into two groups to minimize the energy, but there can be many seemingly sensible divisions with nothing in common.
  • You don’t want the “best” structure, you want the consensus of many good solutions. This is often better than the “best” single solution.
  • If there is no consensus then there is probably nothing there at all.
• The Game of Go: unlike chess, humans remain better at Go than algos (this is true of bridge too).
  • There are simply too many possible options in Go for the traditional approach with explores the entire game tree (as is done in chess).
  • To win, an algo has to assume a player plays randomly beyond the prediction horizon and recomputed the probability of winning a game with each move.
    • This incentivizes (and rewards the algo) for making moves that lead to the most possible winning options, rather than a narrow path which does in fact lead to victory.
    • The goal then becomes broadening the tree as much as possible, and giving the algo player optionality.
    • “Want to evolve evolvability” and not just judge a position, but give mobility (optionality). This is a heuristic in order to gain viability.

How did Ed Thorp Win in Blackjack and the Stock Market?

My earlier post laid out some important lessons on behavioral economics learned from Santa Fe Institute’s conference on Risk: the Human Factor.  The specific lecture that first caught my eye when I saw the roster was Edward Thorp’s discussion on the Kelly Capital Growth Criterion for Risk Control.  I had read the book Fortune’s Formula and was fascinated by one of the core concepts of the book: the Kelly Criterion for capital appreciation. Over time, I have incorporated Kelly into my position-sizing criteria, and was deeply interested in learning from the first man who deployed Kelly in investing.  It's been mentioned that both Warren Buffett and Charlie Munger discussed Kelly with Thorp and used it in their own investment process.  Thus, I felt it necessary to give this particular lecture more attention.

In its simplest form, the Kelly Criterion is stated as follows:

The optimal Kelly wager = (p*(b+1)—1) / b where p is the probability (% chance of an event happening) and b is the odds received upon winning ($b per every $1 wagered).

It was Ed Thorp who first applied the Kelly Criterion in blackjack and then in the stock market.  The following is what I learned from his presentation at SFI. 

Thorp had figured out a strategy for counting cards, but was left wondering how to optimally manage his wager (in investing parlance, we’d call this position sizing).  The goal was a betting approach which would allow for the strategy to be deployed over a long period of time, for a maximized payout.  With the card counting strategy, Thorp in essence was creating a biased coin (a coin toss is your prototypical 50/50 wager, however in a biased coin, the odds are skewed to one side).  This question was approached from a position of how does one deal with risk, rationally?  Finding such a rational risk management strategy was very important, because even with a great strategy in the casino, it was all too easy to go broke before ever attaining successful results.  In other words, if the bets were too big, you would go broke fast, and if the bets were too small you simply would not optimize the payout.

Thorp was introduced to the Kelly formula by his colleague Claude Shannon at MIT.  Shannon was one of the sharpest minds at Bell Labs prior to his stint at MIT and is perhaps best known for his role in discovering/creating/inventing information theory.  While Shannon was at Bell Labs, he worked with a man named John Kelly who wrote a paper called “New Interpretation of Information Rate.”  This paper sought a solution to the problem of a horse racing gambler who receives tips over a noisy phone line.  The gambler can’t quite figure out with complete precision what is said over the fuzzy line; however, he knows enough to make an informed guess, thus imperfectly rigging the odds in his favor. 

What John Kelly did was figure out a way that such a gambler could bet to maximize the exponential rate of the growth of capital.  Kelly observed that in a coin toss, the bet should be equal to one’s edge, and further, as you increase your amount of capital, the rate of growth inevitably declines.

Shannon showed this paper to Thorp presented with a similar problem in blackjack, and Thorp then identified several key features of Kelly (g=growth below):

1. If G>0 then the fortune tends towards infinity.
2. If G<0 then the fortune tends towards 0.
3. If g=0 then Xn oscillates wildly.
4. If another strategy is “essentially different’ then the ratio of Kelly to the different strategy tends towards infinity.
5. Kelly is the single quickest path to an aggregate goal.

This chart illustrates the points:

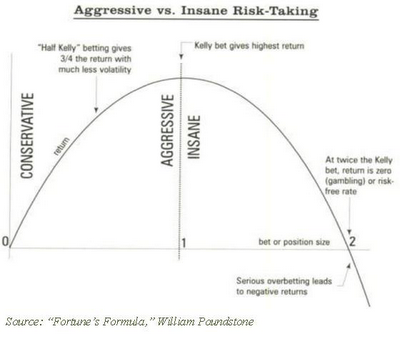
The peak in the middle is the Kelly point, where the optimized wager is situated.  The area to the right of the peak, where the tail heads straight down is in the zone of over-betting, and interestingly, the area to the left of the Kelly peak corresponds directly to the efficient frontier. 

Betting at the Kelly peak yields substantial drawdowns and wild upswings, and as a result is quite volatile on its path to capital appreciation.  Therefore, in essence, the efficient frontier is a path towards making Kelly wagers, while trading some portion of return for lower variance.  As Thorp observed, if you cut your Kelly wager in half, then you can get 3/4s the growth with far less volatility. 

Thorp told the tale of his early endeavors in casinos, and how the casinos scoffed at the notion that he could beat them.  One of the most interesting parts to me was how he felt emotionally despite having confidence in his mathematical edge. Specifically, Thorp felt that the impact of losses placed a heavy psychological burden on his morale, while gains did not have an equal and opposite boost to his psyche.  Further, he said that he found himself stashing some chips in his pocket so as to avoid letting the casino see them (despite the casino having an idea of how many he had outstanding) and possibly as a way to prevent over-betting.  This is somewhat irrational behavior amidst the quest for rational risk management

As the book Bringing Down the House and the movie 21 memorialized, we all know how well Kelly worked in the gambling context.  But how about when it comes to investing?  In 1974, Thorp started a hedge fund called Princeton/Newport Partners, and deployed the Kelly Criterion on a series of non-correlated wagers. To do this, he used warrants and derivatives in situations where they had deviated from the underlying security’s value.  Each wager was an independent wager, and all other exposures, like betas, currencies and interest rates were hedged to market neutrality. 

Princeton/Newport earned 15.8% annualized over its lifetime, with a 4.3% standard deviation, while the market earned 10.1% annualized with a 17.3% standard deviation (both numbers adjusted for dividends).  The returns were great on an absolute basis, but phenomenal on a risk-adjusted basis.  Over its 230 months of operation, money was made in 227 months, and lost in only 3.  All along, one of Thorp’s primary concerns had been what would happen to performance in an extreme event, yet in the 1987 Crash performance continued apace. 

Thorp spent a little bit of time talking about the team from Long Term Capital Management and described their strategy as the anti-Kelly.  The problem with LTCM, per Thorp, was that the LTCM crew “thought Kelly made no sense.”  The LTCM strategy was based on mean reversion, not capital growth, and most importantly, while Kelly was able to generate returns using no leverage, LTCM was “levering up substantially in order to pick up nickels in front of a bulldozer.”

Towards the end of his talk, Thorp told the story of a young Duke student who read his book called Beat the Dealer, about how to deploy Kelly and make money in the casino.  This young Duke student then ventured out to Las Vegas and made a substantial amount of money.  He then read Thorp’s book Beat the Market and went to UC-Irvine, where he used the Kelly formula in convertible debt to again make good money. Ultimately this young built the world’s largest bond fund—Pacific Investment Management Company (PIMCO).  This man was none other than Bill Gross and Thorp drew the important connection between Gross’ risk management as a money manager and his days in the casino.

During the Q&A, Bill Miller, of Legg Mason fame, asked Thorp an interesting two part question: is it more difficult to get an edge in today’s market? And Did LTCM not know tail risk and/or realize the correlations of their bets?  Thorp said that today the market is no more or less difficult than in year’s past.  As for LTCM, Thorp argued that their largest mistake was in failing to recognize that history was not a good boundary (plus the history LTCM looked at was only post-Depression, not age-old) and that without leverage, LTCM did not have a real edge. This is key—LTCM was merely a strategy to deploy leverage, not one to get an edge in the market.

I had the opportunity to ask Thorp a question and I wanted to focus on the emotional element he referenced from the casino days.  My question was:  upon recognizing the force of emotion upon himself, how did he manage to overcome his human emotional impediments and place complete conviction in his formula and strategy?  His answer was a direct reference to Daniel Kahneman’s Thinking, Fast and Slow, whereby he used his system 2, the slow thinking system, in order to force himself to follow the rules outlined by his formulas and process.  Emotion was a human reaction, but there was no room to afford it the opportunity to hinder the powerful force that is mathematics.