My earlier post laid out some important lessons on behavioral economics learned from Santa Fe Institute’s conference on Risk: the Human Factor. The specific lecture that first caught my eye when I saw the roster was Edward Thorp’s discussion on the Kelly Capital Growth Criterion for Risk Control. I had read the book Fortune’s Formula and was fascinated by one of the core concepts of the book: the Kelly Criterion for capital appreciation. Over time, I have incorporated Kelly into my position-sizing criteria, and was deeply interested in learning from the first man who deployed Kelly in investing. It's been mentioned that both Warren Buffett and Charlie Munger discussed Kelly with Thorp and used it in their own investment process. Thus, I felt it necessary to give this particular lecture more attention.
In its simplest form, the Kelly Criterion is stated as follows:
The optimal Kelly wager = (p*(b+1)—1) / b where p is the probability (% chance of an event happening) and b is the odds received upon winning ($b per every $1 wagered).
It was Ed Thorp who first applied the Kelly Criterion in blackjack and then in the stock market. The following is what I learned from his presentation at SFI.
Thorp had figured out a strategy for counting cards, but was left wondering how to optimally manage his wager (in investing parlance, we’d call this position sizing). The goal was a betting approach which would allow for the strategy to be deployed over a long period of time, for a maximized payout. With the card counting strategy, Thorp in essence was creating a biased coin (a coin toss is your prototypical 50/50 wager, however in a biased coin, the odds are skewed to one side). This question was approached from a position of how does one deal with risk, rationally? Finding such a rational risk management strategy was very important, because even with a great strategy in the casino, it was all too easy to go broke before ever attaining successful results. In other words, if the bets were too big, you would go broke fast, and if the bets were too small you simply would not optimize the payout.
Thorp was introduced to the Kelly formula by his colleague Claude Shannon at MIT. Shannon was one of the sharpest minds at Bell Labs prior to his stint at MIT and is perhaps best known for his role in discovering/creating/inventing information theory. While Shannon was at Bell Labs, he worked with a man named John Kelly who wrote a paper called “New Interpretation of Information Rate.” This paper sought a solution to the problem of a horse racing gambler who receives tips over a noisy phone line. The gambler can’t quite figure out with complete precision what is said over the fuzzy line; however, he knows enough to make an informed guess, thus imperfectly rigging the odds in his favor.
What John Kelly did was figure out a way that such a gambler could bet to maximize the exponential rate of the growth of capital. Kelly observed that in a coin toss, the bet should be equal to one’s edge, and further, as you increase your amount of capital, the rate of growth inevitably declines.
Shannon showed this paper to Thorp presented with a similar problem in blackjack, and Thorp then identified several key features of Kelly (g=growth below):
- If G>0 then the fortune tends towards infinity.
- If G<0 then the fortune tends towards 0.
- If g=0 then Xn oscillates wildly.
- If another strategy is “essentially different’ then the ratio of Kelly to the different strategy tends towards infinity.
- Kelly is the single quickest path to an aggregate goal.
This chart illustrates the points:
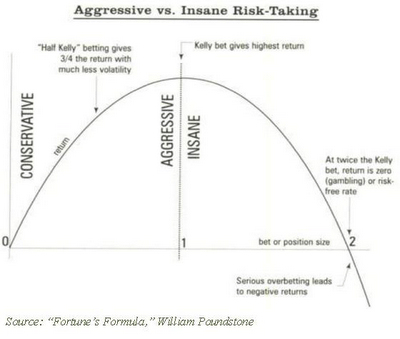
The peak in the middle is the Kelly point, where the optimized wager is situated. The area to the right of the peak, where the tail heads straight down is in the zone of over-betting, and interestingly, the area to the left of the Kelly peak corresponds directly to the efficient frontier.
Betting at the Kelly peak yields substantial drawdowns and wild upswings, and as a result is quite volatile on its path to capital appreciation. Therefore, in essence, the efficient frontier is a path towards making Kelly wagers, while trading some portion of return for lower variance. As Thorp observed, if you cut your Kelly wager in half, then you can get 3/4s the growth with far less volatility.
Thorp told the tale of his early endeavors in casinos, and how the casinos scoffed at the notion that he could beat them. One of the most interesting parts to me was how he felt emotionally despite having confidence in his mathematical edge. Specifically, Thorp felt that the impact of losses placed a heavy psychological burden on his morale, while gains did not have an equal and opposite boost to his psyche. Further, he said that he found himself stashing some chips in his pocket so as to avoid letting the casino see them (despite the casino having an idea of how many he had outstanding) and possibly as a way to prevent over-betting. This is somewhat irrational behavior amidst the quest for rational risk management
As the book Bringing Down the House and the movie 21 memorialized, we all know how well Kelly worked in the gambling context. But how about when it comes to investing? In 1974, Thorp started a hedge fund called Princeton/Newport Partners, and deployed the Kelly Criterion on a series of non-correlated wagers. To do this, he used warrants and derivatives in situations where they had deviated from the underlying security’s value. Each wager was an independent wager, and all other exposures, like betas, currencies and interest rates were hedged to market neutrality.
Princeton/Newport earned 15.8% annualized over its lifetime, with a 4.3% standard deviation, while the market earned 10.1% annualized with a 17.3% standard deviation (both numbers adjusted for dividends). The returns were great on an absolute basis, but phenomenal on a risk-adjusted basis. Over its 230 months of operation, money was made in 227 months, and lost in only 3. All along, one of Thorp’s primary concerns had been what would happen to performance in an extreme event, yet in the 1987 Crash performance continued apace.
Thorp spent a little bit of time talking about the team from Long Term Capital Management and described their strategy as the anti-Kelly. The problem with LTCM, per Thorp, was that the LTCM crew “thought Kelly made no sense.” The LTCM strategy was based on mean reversion, not capital growth, and most importantly, while Kelly was able to generate returns using no leverage, LTCM was “levering up substantially in order to pick up nickels in front of a bulldozer.”
Towards the end of his talk, Thorp told the story of a young Duke student who read his book called Beat the Dealer, about how to deploy Kelly and make money in the casino. This young Duke student then ventured out to Las Vegas and made a substantial amount of money. He then read Thorp’s book Beat the Market and went to UC-Irvine, where he used the Kelly formula in convertible debt to again make good money. Ultimately this young built the world’s largest bond fund—Pacific Investment Management Company (PIMCO). This man was none other than Bill Gross and Thorp drew the important connection between Gross’ risk management as a money manager and his days in the casino.
During the Q&A, Bill Miller, of Legg Mason fame, asked Thorp an interesting two part question: is it more difficult to get an edge in today’s market? And Did LTCM not know tail risk and/or realize the correlations of their bets? Thorp said that today the market is no more or less difficult than in year’s past. As for LTCM, Thorp argued that their largest mistake was in failing to recognize that history was not a good boundary (plus the history LTCM looked at was only post-Depression, not age-old) and that without leverage, LTCM did not have a real edge. This is key—LTCM was merely a strategy to deploy leverage, not one to get an edge in the market.
I had the opportunity to ask Thorp a question and I wanted to focus on the emotional element he referenced from the casino days. My question was: upon recognizing the force of emotion upon himself, how did he manage to overcome his human emotional impediments and place complete conviction in his formula and strategy? His answer was a direct reference to Daniel Kahneman’s Thinking, Fast and Slow, whereby he used his system 2, the slow thinking system, in order to force himself to follow the rules outlined by his formulas and process. Emotion was a human reaction, but there was no room to afford it the opportunity to hinder the powerful force that is mathematics.



